Anatomy of a multipolar neuron.

The biological neuron has its structure like the image above, where it gets the signals from its dendrites and somehow processes this information (we still do not know exactly how it is done), then a spike is fired through its axon, passing the signal through the terminal of the axon to the dendrites of other neurons.

McCulloch-Pitts neuron model.

Based on the biological neuron, Warren McCulloch and Walter Pitts presented the idea of neural networks as computing machines in 1943, creating a fairly simple model of the biological neuron. Each i-th dendrite has an input \(x_i\) which is multiplied by its respectively weight \(w_i\). The result of each dendrite is summed up into a single value, then a bias \(b_i\) is added and passed it through an activation function \(\varphi (\cdot) \) to decide if it fires or not. Writing in matrix form, the weights is a matrix \(W\) that must be transposed to perform the dot product with the input column vector \(X\) plus the bias column vector \(B\), resulting in the following equation: \( \varphi (W^t \cdot X + B) \).

The OR problem is a simple example, but it is intuitive for the first contact with artificial neural networks. Using the MP-neuron, it is possible to solve it by choosing the following weights:

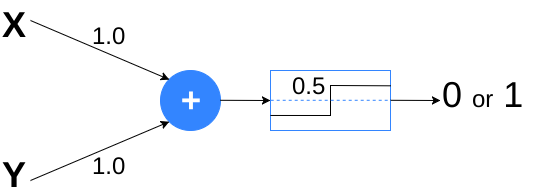OR solution.

Where the bias is equal to zero and the heaviside function is used as an activation function.

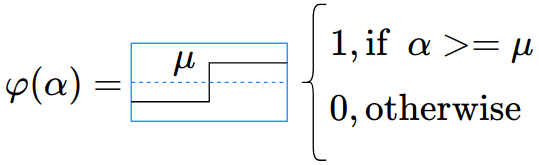Heaviside function.

Which yields a line, i.e. decision boundary, which the data below and above it belongs to the classes 0 and 1 respectively. The figure below illustrates the situation:

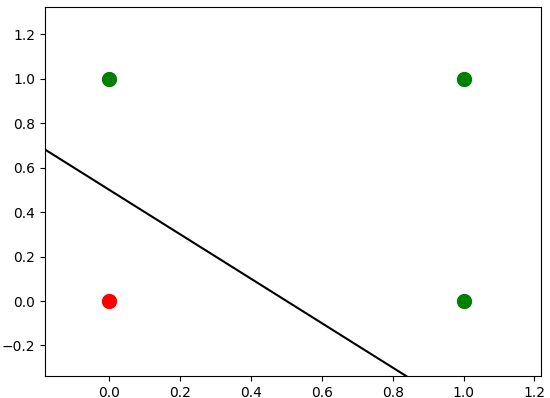Graphical solution of the OR problem.

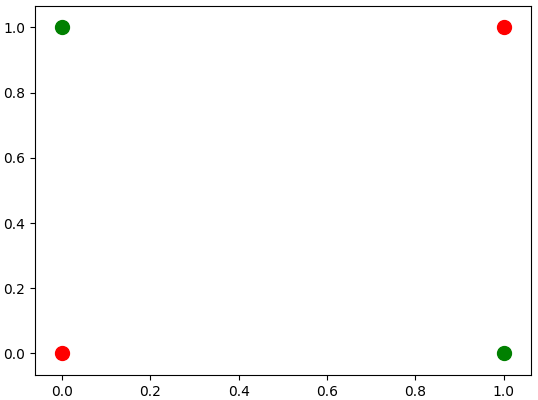XOR problem.

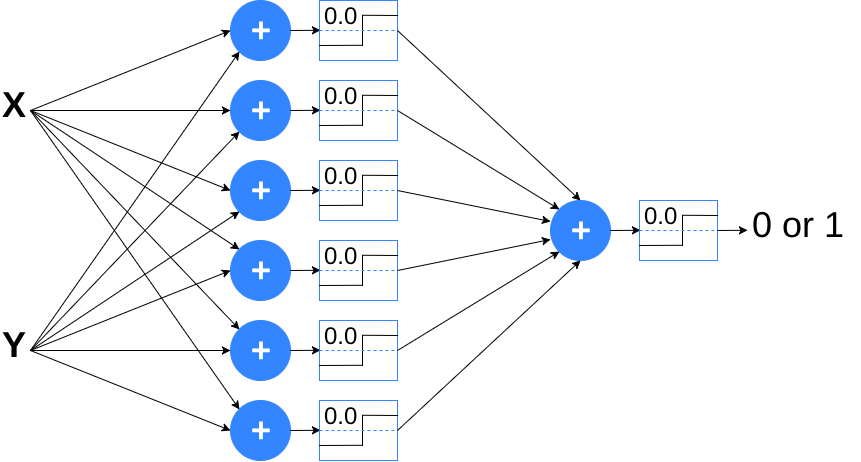
Note that the XOR can not be splitted by one straight line and, since the MP-neuron gives the possibility to draw only a straight line, i.e. a linear equation, is necessary to use more than one MP-neuron and also, change the architecture of the network. The strategy is to map the data to other space, thus the first layer will have the role to map the data to another space. First, isolating the outside point, the following line is desired to be a decision boundary:

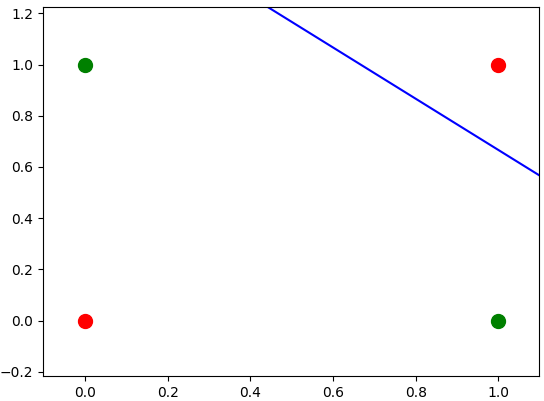Isolating the (1, 1) data.

This is obtained by the MP-neuron below:

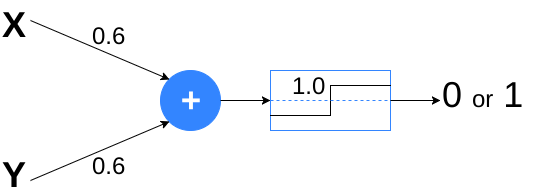MP-neuron that isolates the (1,1) data.

Then, to isolate the other red point, the pink line is added to be another decision boundary:

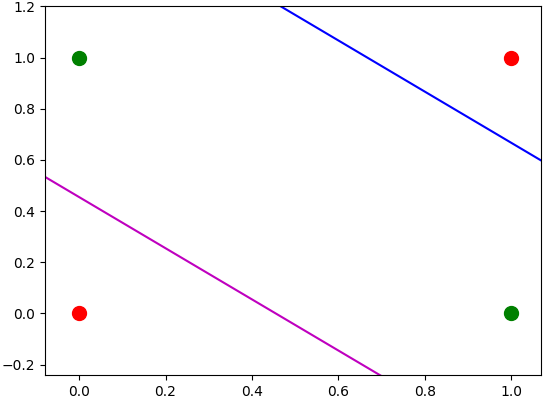Isolating the (0,0) data.

This is obtained by the following MP-neuron:

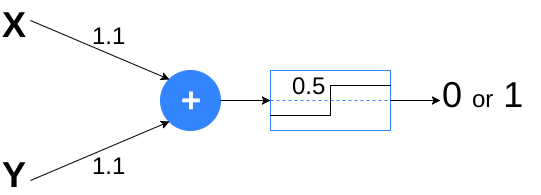MP-neuron that isolates the (0,0) data.

Merging the two MP-neurons, it yields a function of mapping \(f : (X,Y) \rightarrow (X’,Y’)\):

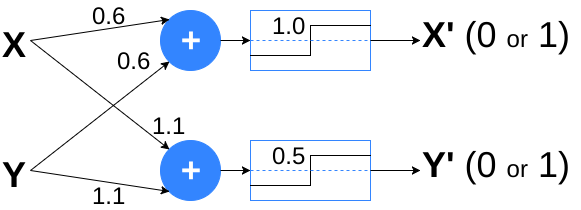Layer that maps the data to another space.

Which gives the following mapping of the data:

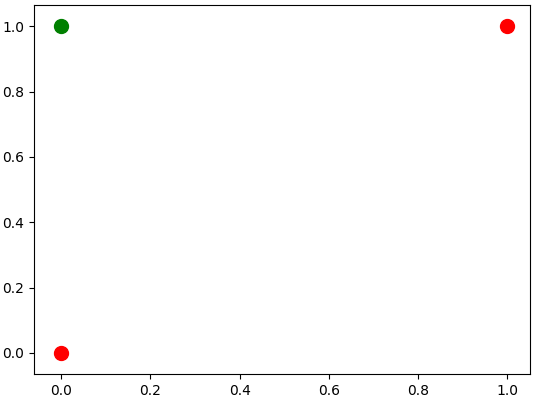Result of the mapping.

Note that now, the values \((0,1)\) and \((1,0)\) from the original space are overlapped in this new space on \((0,1)\), and now the data can be separated by a straight line. Thus, the work now is to find the linear equation that represents it, which can be the equation \(Y’ = X’ + 0.5\):

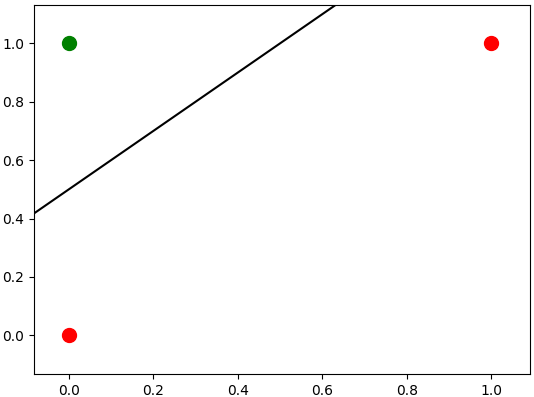Graphical solution of the XOR problem.

Putting it all together:

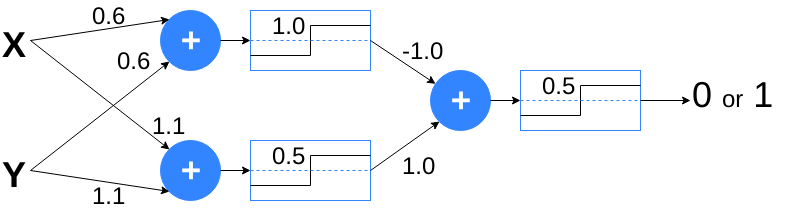XOR solution.

In these examples, the artificial neural networks was trained by hand, which does not make it powerful since it can spent a lot of time to do it and for more complex problems it turns infeasible.

For this task, was trained an Artificial Neural Network (ANN) to play the Flappy Bird game (inspired by this post) and it was chosen the representation of a chromosome as real values to represent the weights of the network.

Architecture of the ANN used.

The architecture of the neural network used is shown above, and the bird will flap or not if the output is 1 or 0, respectively.

Meaning of the ANN inputs.

The X is the horizontal distance between the bird and the center of the wall and the Y is the vertical distance between the bird and the center of the gap in the wall. The fitness used in the genetic algorithm is the total distance traveled by the bird.

Training the ANN to play the Flappy Bird game.

The video above was captured while training the network. To increase the difficulty over time, the speed was increased every 10 seconds.


Checkout the code on GitHub.